When an object is physical, the script function
causes an object to drift smoothly toward a target position. The drawback is that the motion is not uniform. The velocity decreases toward zero as the target is approached.
This movement is approximated by
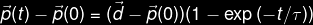
The object is at position
at time t. Because of the exponential attenuation of the velocity, it will reach the position 
after several intervals of the time interval 
. The object motion is made more uniform by using only an early portion of this exponential motion.
To create this effect, calculate a target position
which lays beyond , then terminate the movement at the time . In algebraic terms, solve this equation for :
The solution is
where e is the base of the natural logarithms, 2.7182818284....
For a target position d_target, a single step movement is shown below as code fragments.
float tau = 4;
A more nuanced implementation would declare a list of d_target positions. The timer event would move thought the list, calculating a series of D_targets, then using llMoveToTarget(). At the end of the list, the timer event would either return to the beginning of the list, or use llStopMoveToTarget().
Des.de.mona
[end]
For a target position d_target, a single step movement is shown below as code fragments.
float tau = 4;
vector d_target = <110,200,30>;
float e = 2.7182818284;
touch_start( integer nTouch ) {
float f = e / ( e - 1 );
vector D_target = llGetPos() + f *( d_target - llGetPos() );
llMoveToTarget( D_target, tau );
llSetTimerEvent( tau );
}
timer() {
llStopMoveToTarget();
llSetTimerEvent( 0 );
}
A more nuanced implementation would declare a list of d_target positions. The timer event would move thought the list, calculating a series of D_targets, then using llMoveToTarget(). At the end of the list, the timer event would either return to the beginning of the list, or use llStopMoveToTarget().
Des.de.mona
[end]
