Uniform Motion Using llMoveToTarget

When an object is physical, the script function

causes an object to drift smoothly toward a target position.  The drawback is that the motion is not uniform.  The velocity decreases toward zero as the target is approached.

  

This movement is approximated by

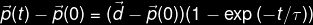
The object is at position at time t.  Because of the exponential attenuation of the velocity, it will reach the position after several intervals of the time interval .  

                                                                                                                              
The object motion is made more uniform by using only an early portion of this exponential motion.

To create this effect, calculate a target position which lays beyond , then terminate the movement at the time .   In algebraic terms, solve this equation for :

The solution is

 

where e is the base of the natural logarithms, 2.7182818284....

                                                                                                                               
For a target position d_target, a single step movement is shown below as code fragments.

float tau = 4;

vector d_target = <110,200,30>;

float e = 2.7182818284;
 

touch_start( integer nTouch ) {

    float f = e / ( e - 1 );

    vector D_target = llGetPos() + f *( d_target - llGetPos() );

    llMoveToTarget( D_target, tau );

    llSetTimerEvent( tau );

}

timer() {

    llStopMoveToTarget();

    llSetTimerEvent( 0 );

}

A more nuanced implementation would declare a list of d_target positions.  The timer event would move thought the list, calculating a series of D_targets, then using llMoveToTarget().  At the end of the list, the timer event would either return to the beginning of the list, or use llStopMoveToTarget().


Des.de.mona

[end]

Embedding Equations

Given that blogspot does not intrinsically support equations, I am experimenting with the LaTeX converter found at codecogs.

While this relies on the continued existence of the codecogs website, the countervailing advantage of this method is that the LaTeX input statement used to generate an equation becomes embedded in the web page.   For example, if you look at the source of this web page, you will see that the above equation for the derivative of the natural logarithm is generated using this statement:

\frac{d}{dx}\ln(x)=\frac{1}{x}

Should codecogs cease to exist, the LateX input statement has been preserved and may be used with any converter to regenerate the typeset image.  As for LaTeX itself, it is one of those Unix things that has been around for 30 years and is now distributed under the LaTeX Project Public License.

Des.de.mona